16 May 2020

Jupyter Notebook is one of the most useful tool for data exploration, machine learning and fast prototyping. There are many plugins and projects which make it even more powerful:
But sometimes you simply need IDE …
One of my favorite text editor is vim. It is lightweight, fast and with appropriate plugins it can be used as a IDE.
Using Dockerfile you can build jupyter environment with fully equipped vim:
FROM continuumio/miniconda3
RUN apt update && apt install curl git cmake ack g++ python3-dev vim-youcompleteme tmux -yq
RUN sh -c "$(curl -fsSL https://raw.githubusercontent.com/qooba/vim-python-ide/master/setup.sh)"
RUN conda install xeus-python jupyterlab jupyterlab-git -c conda-forge
RUN jupyter labextension install @jupyterlab/debugger @jupyterlab/git
RUN pip install nbdev
RUN echo "alias ls='ls --color=auto'" >> /root/.bashrc
CMD bin/bash
Now you can run the image:
docker run --name jupyter -d --rm -p 8888:8888 -v $(pwd)/jupyter:/root/.jupyter -v $(pwd)/notebooks:/opt/notebooks qooba/miniconda3 /bin/bash -c "jupyter lab --notebook-dir=/opt/notebooks --ip='0.0.0.0' --port=8888 --no-browser --allow-root --NotebookApp.password='' --NotebookApp.token=''"
In the jupyter lab start terminal session, run bash (it works better in bash) and then vim.
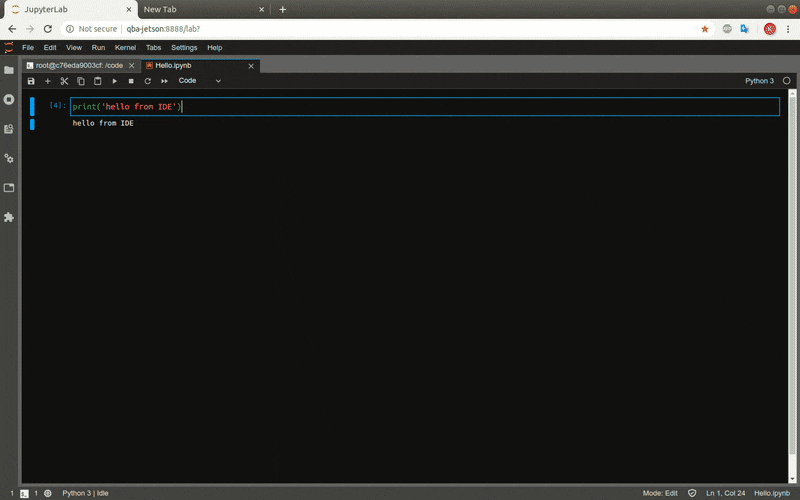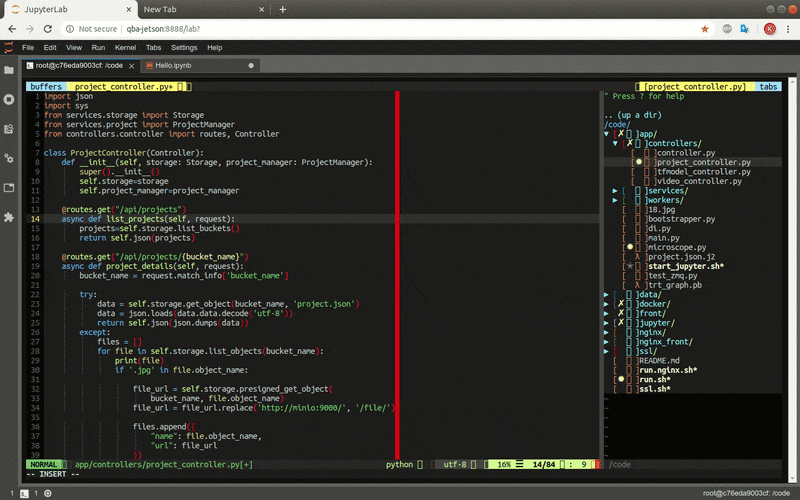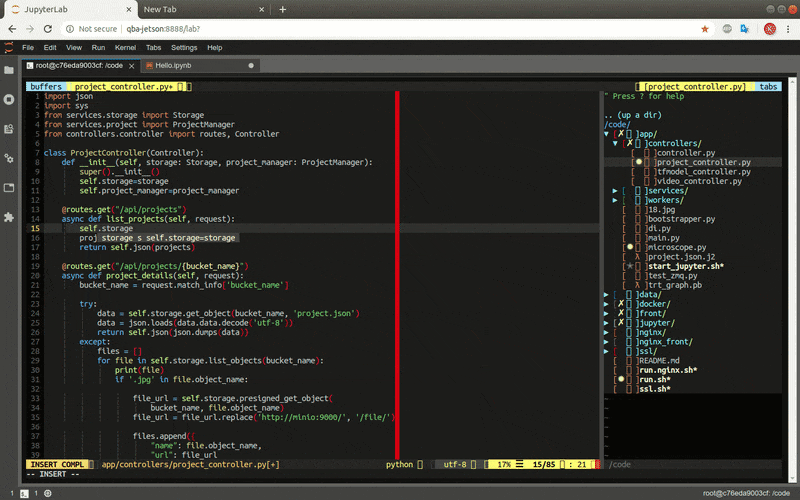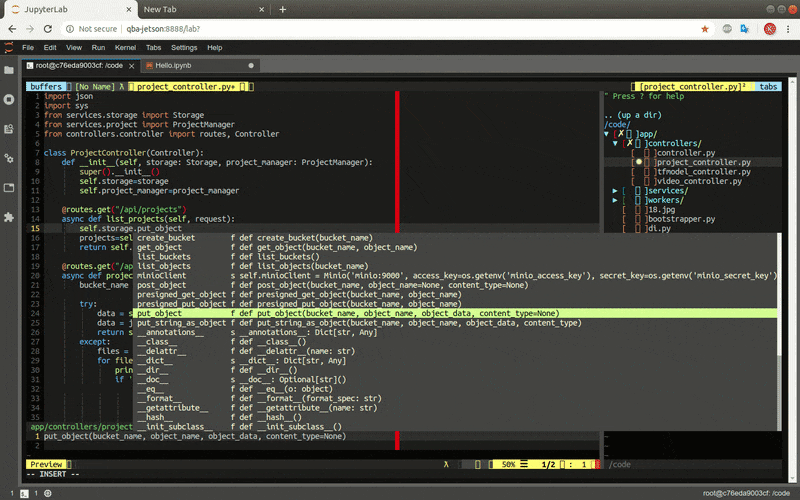
The online IDE is ready:
References
[1] Top image Boskampi from Pixabay
10 May 2020

IoT and AI are the hottest topics nowadays which can meet on Jetson Nano device.
In this article I’d like to show how to use FastAI library, which is built on the top of the PyTorch on Jetson Nano. Additionally I will show how to optimize the FastAI model for the usage with TensorRT.
You can find the code on https://github.com/qooba/fastai-tensorrt-jetson.git.
1. Training
Although the Jetson Nano is equipped with the GPU it should be used as a inference device rather than for training purposes. Thus I will use another PC with the GTX 1050 Ti for the training.
Docker gives flexibility when you want to try different libraries thus I will use the image which contains the complete environment.
Training environment Dockerfile:
FROM nvcr.io/nvidia/tensorrt:20.01-py3
WORKDIR /
RUN apt-get update && apt-get -yq install python3-pil
RUN pip3 install jupyterlab torch torchvision
RUN pip3 install fastai
RUN DEBIAN_FRONTEND=noninteractive && apt update && apt install curl git cmake ack g++ tmux -yq
RUN pip3 install ipywidgets && jupyter nbextension enable --py widgetsnbextension
CMD ["sh","-c", "jupyter lab --notebook-dir=/opt/notebooks --ip='0.0.0.0' --port=8888 --no-browser --allow-root --NotebookApp.password='' --NotebookApp.token=''"]
To use GPU additional nvidia drivers (included in the NVIDIA CUDA Toolkit) are needed.
If you don’t want to build your image simply run:
docker run --gpus all --name jupyter -d --rm -p 8888:8888 -v $(pwd)/docker/gpu/notebooks:/opt/notebooks qooba/fastai:1.0.60-gpu
Now you can use pets.ipynb notebook (the code is taken from lesson 1 FastAI course) to train and export pets classification model.
from fastai.vision import *
from fastai.metrics import error_rate
# download dataset
path = untar_data(URLs.PETS)
path_anno = path/'annotations'
path_img = path/'images'
fnames = get_image_files(path_img)
# prepare data
np.random.seed(2)
pat = r'/([^/]+)_\d+.jpg$'
bs = 16
data = ImageDataBunch.from_name_re(path_img, fnames, pat, ds_tfms=get_transforms(), size=224, bs=bs).normalize(imagenet_stats)
# prepare model learner
learn = cnn_learner(data, models.resnet34, metrics=error_rate)
# train
learn.fit_one_cycle(4)
# export
learn.export('/opt/notebooks/export.pkl')
Finally you get pickled pets model (export.pkl).
2. Inference (Jetson Nano)
The Jetson Nano device with Jetson Nano Developer Kit already comes with the docker thus I will use it to setup the inference environment.
I have used the base image nvcr.io/nvidia/l4t-base:r32.2.1 and installed the pytorch and torchvision.
If you have JetPack 4.4 Developer Preview you can skip this steps and start with the base image nvcr.io/nvidia/l4t-pytorch:r32.4.2-pth1.5-py3.
The FastAI installation on Jetson is more problematic because of the blis package. Finally I have found the solution here.
Additionally I have installed torch2trt package which converts PyTorch model to TensorRT.
Finally I have used the tensorrt from the JetPack which can be found in
/usr/lib/python3.6/dist-packages/tensorrt .
The final Dockerfile is:
FROM nvcr.io/nvidia/l4t-base:r32.2.1
WORKDIR /
# install pytorch
RUN apt update && apt install -y --fix-missing make g++ python3-pip libopenblas-base
RUN wget https://nvidia.box.com/shared/static/ncgzus5o23uck9i5oth2n8n06k340l6k.whl -O torch-1.4.0-cp36-cp36m-linux_aarch64.whl
RUN pip3 install Cython
RUN pip3 install numpy torch-1.4.0-cp36-cp36m-linux_aarch64.whl
# install torchvision
RUN apt update && apt install libjpeg-dev zlib1g-dev git libopenmpi-dev openmpi-bin -yq
RUN git clone --branch v0.5.0 https://github.com/pytorch/vision torchvision
RUN cd torchvision && python3 setup.py install
# install fastai
RUN pip3 install jupyterlab
ENV TZ=Europe/Warsaw
RUN ln -snf /usr/share/zoneinfo/$TZ /etc/localtime && echo $TZ > /etc/timezone && apt update && apt -yq install npm nodejs python3-pil python3-opencv
RUN apt update && apt -yq install python3-matplotlib
RUN git clone https://github.com/NVIDIA-AI-IOT/torch2trt.git /torch2trt && mv /torch2trt/torch2trt /usr/local/lib/python3.6/dist-packages && rm -r /torch2trt
COPY tensorrt /usr/lib/python3.6/dist-packages/tensorrt
RUN pip3 install --no-deps fastai
RUN git clone https://github.com/fastai/fastai /fastai
RUN apt update && apt install libblas3 liblapack3 liblapack-dev libblas-dev gfortran -yq
RUN curl -LO https://github.com/explosion/cython-blis/files/3566013/blis-0.4.0-cp36-cp36m-linux_aarch64.whl.zip && unzip blis-0.4.0-cp36-cp36m-linux_aarch64.whl.zip && rm blis-0.4.0-cp36-cp36m-linux_aarch64.whl.zip
COPY blis-0.4.0-cp36-cp36m-linux_aarch64.whl .
RUN pip3 install scipy pandas blis-0.4.0-cp36-cp36m-linux_aarch64.whl spacy fastai scikit-learn
CMD ["sh","-c", "jupyter lab --notebook-dir=/opt/notebooks --ip='0.0.0.0' --port=8888 --no-browser --allow-root --NotebookApp.password='' --NotebookApp.token=''"]
As before you can skip the docker image build and use ready image:
docker run --runtime nvidia --network app_default --name jupyter -d --rm -p 8888:8888 -e DISPLAY=$DISPLAY -v /tmp/.X11-unix/:/tmp/.X11-unix -v $(pwd)/docker/jetson/notebooks:/opt/notebooks qooba/fastai:1.0.60-jetson
Now we can open jupyter notebook on jetson and move pickled model file export.pkl from PC.
The notebook jetson_pets.ipynb show how to load the model.
import torch
from torch2trt import torch2trt
from fastai.vision import *
from fastai.metrics import error_rate
learn = load_learner('/opt/notebooks/')
learn.model.eval()
model=learn.model
if torch.cuda.is_available():
input_batch = input_batch.to('cuda')
model.to('cuda')
Additionally we can optimize the model using torch2trt package:
x = torch.ones((1, 3, 224, 224)).cuda()
model_trt = torch2trt(learn.model, [x])
Let’s prepare example input data:
import urllib
url, filename = ("https://github.com/pytorch/hub/raw/master/dog.jpg", "dog.jpg")
try: urllib.URLopener().retrieve(url, filename)
except: urllib.request.urlretrieve(url, filename)
from PIL import Image
from torchvision import transforms
input_image = Image.open(filename)
preprocess = transforms.Compose([
transforms.Resize(256),
transforms.CenterCrop(224),
transforms.ToTensor(),
transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225]),
])
input_tensor = preprocess(input_image)
input_batch = input_tensor.unsqueeze(0)
Finally we can run prediction for PyTorch and TensorRT model:
x=input_batch
y = model(x)
y_trt = model_trt(x)
and compare PyTorch and TensorRT performance:
def prediction_time(model, x):
import time
times = []
for i in range(20):
start_time = time.time()
y_trt = model(x)
delta = (time.time() - start_time)
times.append(delta)
mean_delta = np.array(times).mean()
fps = 1/mean_delta
print('average(sec):{},fps:{}'.format(mean_delta,fps))
prediction_time(model,x)
prediction_time(model_trt,x)
where for:
- PyTorch - average(sec):0.0446, fps:22.401
- TensorRT - average(sec):0.0094, fps:106.780
The TensorRT model is almost 5 times faster thus it is worth to use torch2trt.
References
[1] Top image DrZoltan from Pixabay
12 May 2019

With big pleasure I would like to invite you to join Azuronet - .NET & Azure Meetup #2 in Warsaw, where I will talk (in polish) about Milla project and give you some insights into the world of chatbots and intelligent assistants.
01 May 2019

I am pleased to hear that the first Polish banking chatbot with which you can make a transfer was awarded in a competition organized by a Gazeta Bankowa. With Milla you can talk in the Bank Millennium mobile application. Currently, Milla can speak (text to speech), listen (automatic speak recognition) and understand what you write to her (intent detection with slot filling).
This is not a sponsored post :) but I’ve been developing Milla for the few months and I’m really happy that I had opportunity to do this.
Have a nice talk with Milla.
09 Feb 2019

Quantum computing nowadays is the one of the hottest topics in the computer science world.
Recently IBM unveiled the IBM Q System One: a 20-qubit quantum computer which is touting as “the world’s first fully integrated universal quantum computing system designed for scientific and commercial use”.
In this article I’d like how to show the quantum teleportation phenomenon. I will use the Q# language designed by Microsoft to simplify creating quantum algorithms.
In this example I have used the quantum simulator which I have wrapped with the REST api and put into the docker image.
Quantum teleportation allows moving a quantum state from one location to another. Shared quantum entanglement between two particles in the sending and receiving locations is used to do this without having to move physical particles along with it.
1. Theory
Let’s assume that we want to send the message, specific quantum state described using Dirac notation:
| [latex display=”true”] |
\psi\rangle=\alpha |
0\rangle+\beta |
1\rangle[/latex] |
Additionally we have two entangled qubits, first in Laboratory 1 and second in Laboratory 2:
| [latex display=”true”] |
\phi^+\rangle=\frac{1}{\sqrt{2}}( |
00\rangle+ |
11\rangle)[/latex] |
thus we starting with the input state:
| [latex display=”true”] |
\psi\rangle |
\phi^+\rangle=(\alpha |
0\rangle+\beta |
1\rangle)(\frac{1}{\sqrt{2}}( |
00\rangle+ |
11\rangle))[/latex] |
| [latex display=”true”] |
\psi\rangle |
\phi^+\rangle=\frac{\alpha}{\sqrt{2}} |
000\rangle + \frac{\alpha}{\sqrt{2}} |
011\rangle + \frac{\beta}{\sqrt{2}} |
100\rangle + \frac{\beta}{\sqrt{2}} |
111\rangle [/latex] |
To send the message we need to start with two operations applying CNOT and then Hadamard gate.
CNOT gate flips the second qubit only if the first qubit is 1.
Applying CNOT gate will modify the first qubit of the input state and will result in:
| [latex display=”true”]\frac{\alpha}{\sqrt{2}} |
000\rangle + \frac{\alpha}{\sqrt{2}} |
011\rangle + \frac{\beta}{\sqrt{2}} |
110\rangle + \frac{\beta}{\sqrt{2}} |
101\rangle[/latex] |
Hadamard gate changes states as follows:
| [latex display=”true”] |
0\rangle \rightarrow \frac{1}{\sqrt{2}}( |
0\rangle+ |
1\rangle))[/latex] |
and
| [latex display=”true”] |
1\rangle \rightarrow \frac{1}{\sqrt{2}}( |
0\rangle- |
1\rangle))[/latex] |
Applying Hadmard gate results in:
| [latex display=”true”]\frac{\alpha}{\sqrt{2}}(\frac{1}{\sqrt{2}}( |
0\rangle+ |
1\rangle)) |
00\rangle + \frac{\alpha}{\sqrt{2}}(\frac{1}{\sqrt{2}}( |
0\rangle+ |
1\rangle)) |
11\rangle + \frac{\beta}{\sqrt{2}}(\frac{1}{\sqrt{2}}( |
0\rangle- |
1\rangle)) |
10\rangle + \frac{\beta}{\sqrt{2}}(\frac{1}{\sqrt{2}}( |
0\rangle- |
1\rangle)) |
01\rangle[/latex] |
and:
| [latex display=”true”]\frac{1}{2}(\alpha |
000\rangle+\alpha |
100\rangle+\alpha |
011\rangle+\alpha |
111\rangle+\beta |
010\rangle-\beta |
110\rangle+\beta |
001\rangle-\beta |
101\rangle)[/latex] |
which we can write as:
| [latex display=”true”]\frac{1}{2}( |
00\rangle(\alpha |
0\rangle+\beta |
1\rangle)+ |
01\rangle(\alpha |
1\rangle+\beta |
0\rangle)+ |
10\rangle(\alpha |
0\rangle-\beta |
1\rangle)+ |
11\rangle(\alpha |
1\rangle-\beta |
0\rangle))[/latex] |
Then we measure the states of the first two qubits (message qubit and Laboratory 1 qubit) where we can have four results:
-
| [latex] |
00\rangle[/latex] which simplifies equation to: [latex] |
00\rangle(\alpha |
0\rangle+\beta |
1\rangle)[/latex] and indicates that the qubit in the Laboratory 2 is [latex]\alpha |
0\rangle+\beta |
1\rangle[/latex] |
-
| [latex] |
01\rangle[/latex] which simplifies equation to: [latex] |
01\rangle(\alpha |
1\rangle+\beta |
0\rangle)[/latex] and indicates that the qubit in the Laboratory 2 is [latex]\alpha |
1\rangle+\beta |
0\rangle[/latex] |
-
| [latex] |
10\rangle[/latex] which simplifies equation to: [latex] |
10\rangle(\alpha |
0\rangle-\beta |
1\rangle)[/latex] and indicates that the qubit in the Laboratory 2 is [latex]\alpha |
0\rangle-\beta |
1\rangle[/latex] |
-
| [latex] |
11\rangle[/latex] which simplifies equation to: [latex] |
11\rangle(\alpha |
1\rangle-\beta |
0\rangle)[/latex] and indicates that the qubit in the Laboratory 2 is [latex]\alpha |
1\rangle-\beta |
0\rangle[/latex] |
Now we have to send the result classical way from Laboratory 1 to Laboratory 2.
Finally we know what transformation we need to apply to qubit in the Laboratory 2
to make its state equal to message qubit:
| [latex display=”true”] |
\psi\rangle=\alpha |
0\rangle+\beta |
1\rangle[/latex] |
if Laboratory 2 qubit is in state:
-
| [latex]\alpha |
0\rangle+\beta |
1\rangle[/latex] we don’t need to do anything. |
-
| [latex]\alpha |
1\rangle+\beta |
0\rangle[/latex] we need to apply NOT gate. |
-
| [latex]\alpha |
0\rangle-\beta |
1\rangle[/latex] we need to apply Z gate. |
-
| [latex]\alpha |
1\rangle-\beta |
0\rangle[/latex] we need to apply NOT gate followed by Z gate |
This operations will transform Laboratory 2 qubit state to initial message qubit state thus we moved the particle state from Laboratory 1 to Laboratory 2 without moving particle.
2. Code
Now it’s time to show the quantum teleportation using Q# language. I have used Microsoft Quantum Development Kit to run the Q# code inside the .NET Core application. Additionally I have added the nginx proxy with the angular gui which will help to show the results.
Everything was put inside the docker to simplify the setup.
Before you will start you will need git, docker and docker-compose installed on your machine (https://docs.docker.com/get-started/)
To run the project we have to clone the repository and run it using docker compose:
git clone https://github.com/qooba/quantum-teleportation-qsharp.git
cd quantum-teleportation-qsharp
docker-compose -f app/docker-compose.yml up
Now we can run the http://localhost:8020/ in the browser:
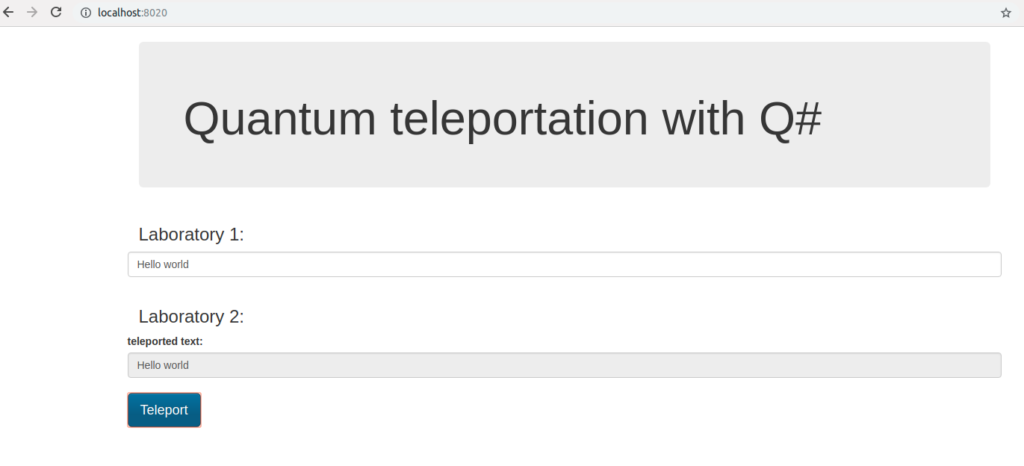
Then we can put the message in the Laboratory 1, click the Teleport button, trigger for the teleportation process which sends the message to the Laboratory 2.
The text is converted into array of bits and each bit is sent to the Laboratory 2 using quantum teleportation.
In the first step we encode the incoming message using X gate.
if (message) {
X(msg);
}
Then we prepare the entanglement between the qubits in the Laboratory 1 and Laboratory 2.
H(here);
CNOT(here, there);
In the second step we apply CNOT and Hadamard gate to send the message:
CNOT(msg, here);
H(msg);
Finally we measure the message qubit and the Laboratory 1 qubit:
if (M(msg) == One) {
Z(there);
}
if (M(here) == One) {
X(there);
}
| If the message qubit has state [latex] |
1\rangle[/latex] then we need to apply the Z gate to the Laboratory 2 qubit. |
| If the Laboratory 1 qubit has state [latex] |
1\rangle[/latex] then we need to apply the X gate to the Laboratory 2 qubit. This information must be sent classical way to the Laboratory 2. |
Now the Laboratory 2 qubit state is equal to the initial message qubit state and we can check it:
if (M(there) == One) {
set measurement = true;
}
This kind of communication is secure because even if someone will take over the information sent classical way it is still impossible to decode the message.






